Зачем нужен Multiplexed Metropolis Light Transport (MMLT)?

Metropolis Light Transport, реализованный ранее в Hydra Renderer, называетеся иногда Kelemen Metropolis Light Transport (KMLT) по имени учёного его придумавшего. Или Primary Sample Space MLT (PSSMLT) по принципу действия (он работает в т. н. первичном пространстве путей, Primary Sample Space (рис. 1)). К сожалению, Kelemen MLT сам по себе имеет ряд недостатков:

1. Он однонаправленный. Трассировка производится только из камеры, из-за чего не все возможные стратегии используются. То есть можно интегрировать эффективнее.
2. Не работает с микрорельемом (шумит на нём). Это в некотором смысле следствие первого пункта. Происходит это из-за того что малое изменение чисел в первичном пространстве путей при наличие микрорельтефа всегда приводит к большому изменению в мировом пространстве путей. Просто потому что направление отражения считается всегда относительно нормали. В двунаправленном MLT за счёт того что есть мутация пути от источника (light mutation), явная стратегия (соединение теневым лучом) "вывозит" ситуацию с микро-рельефом.
3. Двунаправленный (Bidirectional, BPT) Kelemn MLT, решая проблему номер 2, с другой стороны, обладает иными недостатками. Он обладает повышенным начальным смещением (startup bias) т. к. каждый шаг в нём значительно дороже чем в однонаправленном KMLT. Далее, в двунаправленном KMLT сам алгоритм Метрополиса в некотором смысле конкурирует с многократной выборкой по значимости (MIS). Более того, основной недостатой MIS, заключающийся в том что лишь 1-2 пути из 10 вносят существенный вклад, лишь усиливается благодаря алгоритму Метрополиса.
4. Классический BPT требует хранения всех вершин пути в памяти и его компактная реализациая на GPU затруднена.

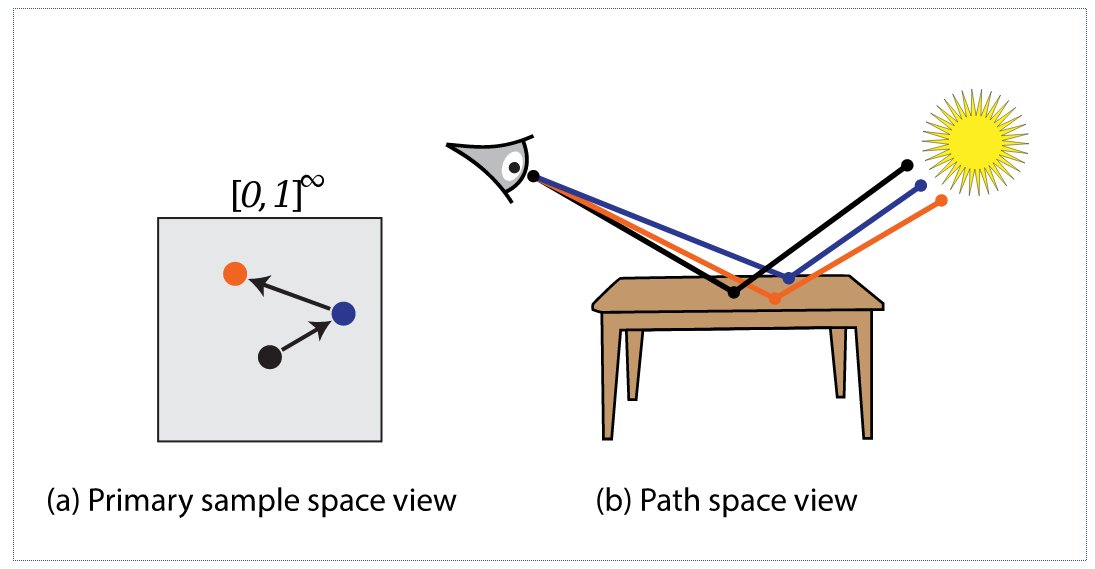
Рисунок 1. Иллюстрация первичного пространства путей (a) и мирового пространства путей (b). В Kelemen MLT марковская цепь блуждает в первичном пространстве путей, а при построении путей неявным образом происходит преобразованние из (a) в (b).

В чём преимущества MMLT?

Необходимо отметить, что многократная выборка по значимости (MIS) и алгоритм Метрополиса могут и должны использоваться вместе. Однако это можно сделать разными способами. Ключ к успеху MMLT лежит в построении такого пространства интегрирования, в котором алгоритм Метрополиса и многократная выборка по значимости не конкурируют, а усиливают друг друга.

Для того чтобы комбинировать алгоритм Метрополиса и многократную выборку по значимости более эффективно, в MMLT строится т. н. "мультиплексированное" пространство интегрирования. Это происходит путём добавления двух степеней свободы --- (1) глубины трассировки d и (2) стратегии сэмплирования пути s. Далее марковская цепь статистически находит оптимальный способ построения пути в BPT, варьируя параметр s (рис. 2).

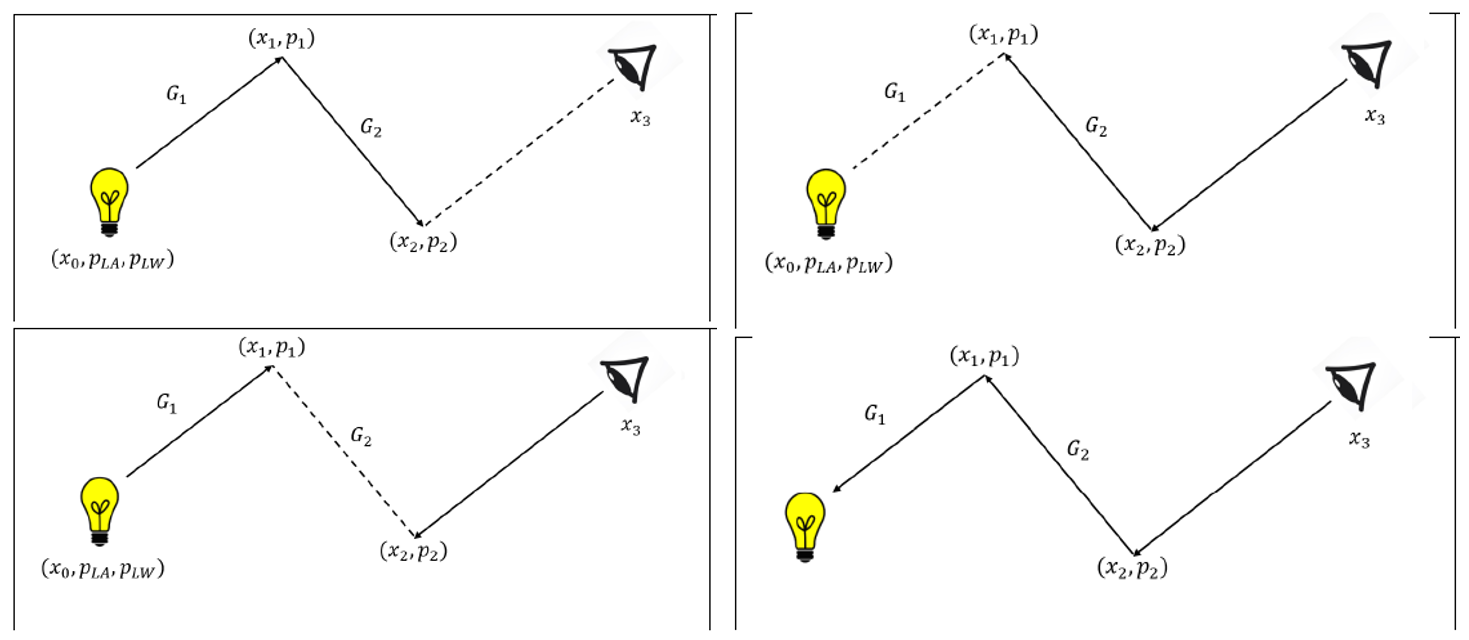
Рисунок 2. Пример 4-ёх стратегий для глубины трассировки, равной 3. Пунктирная черта изображает явное соединение вершин. Оптимимальный выбор стратегии происходит автоматически алгоритмом Метрополиса, т.к. функция вклада в MMLT построена в виде взвешенной суммы различных стратегий.

Благодаря этому алгоритм Метрополиса автоматически перераспределяет вычислительные ресурсы таким образом, что малозначимые стратегии и соединения в BPT считаются редко. Причём это происходит в том числе и с учётом функции видимости, т. к. алгоритм Метрополиса строит распределение пропорционально итоговому ответу. Более передовые методы, как правило, построены поверх MMLT и нацелены на его улучшение или устранение его проблем. Эти проблемы происходят из того, что "мультиплексированное" пространство интегрирования в MMLT, благодаря которому алгоритм Метрополиса и многократная выборка по значимости хорошо работают в связке, само по себе более сложно (т. е. вероятность попадания в существенную область пространства равномерно случайной выборкой в нём меньше), чем первичное пространство путей в Kelemen MLT из-за априорного разбиения ("мультиплексирования") путей по глубине и стратегиям.

Сравнение с Octane

Сиcтема Octane была выбрана по 2 основным причинам. Во-первых, Octane активно позиционируется разработчиком как самая быстрая в мире рендер-система. Во-вторых, в настоящий момент Octane --- единственная в мире рендер-система на GPU, в которой реализован и используется на практике MCMC-метод интегрирования освещённости --- ERPT/PMC.

Сравнение с рендер-системой Octane (версия 4.00--6.10) проводилось на машине с 2 GPU фирмы Nvidia (RTX2070 и GTX1070), ОС Windows 7. Эталоны были получены за 3 часа и использовались для оценки ошибки. Изображения эталонов для данного сравнения в не представлены.

Было проведено также сравнение скорости трассировки лучей (оценивая количество сэмплов в секунду). К счастью это легко сделать т. к. обе сопоставляемые программы позволяют фиксировать количество Монте-Карло сэмплов в PT и глубину просчёта. Замерив время, за которое это число сэмплов было сделано, можно оценить скорость (таблица 1).

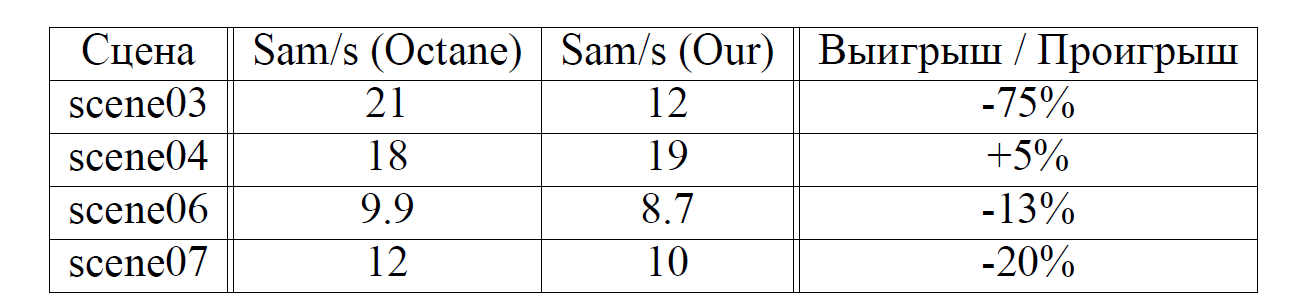
Таблица 1. Сравнение скорости трассировки лучей в системе Octane и в разработанной системе при фиксированной глубине просчёта в PT, равной 8 отскоков. В таблице отображено количество Монте-Карло сэмплов в секунду. Количество обрабатываемых лучей в секунду нетрудно оценить если умножить это число на 16. Протестировано на Nvidia GTX2070. Для этого сравнения в Octane денойзинг и тон-маппинг на GPU были отключены чтобы оценить чистую производительность геометрического ядра системы.

Рисунок 3. Сравнение с Octane.

Рисунок 4. Сравнение с Octane.

Рисунок 3. Сравнение с Octane.